티스토리 뷰
차원이란?
공간 내에 있는 점 등의 위치를 나타내기 위해 필요한 축의 개수
차원의 수 증가 = 변수의 수 증가 = 데이터를 표현하는 공간 증가
3개의 특징을 사용하는 데이터 셋 = 3차원
ex) 키, 몸무게, 발 크기 3개의 특징을 가진 데이터 셋은 3차원의 표현이 필요하다.
차원의 저주
차원의 수가 늘어나 차원이 커지면서 발생하는 문제
학습 데이터 수가 차원의 수보다 작을 경우 성능이 저하 된다.
데이터 수는 그대로인데 차원이 증가하면 빈 공간이 생긴다. -> 데이터 간의 간격이 늘어난다. -> 과적합 발생
ex)2차원 평면인 데이터셋에서 3차원이 되면 데이터의 밀도가 낮아진다.
차원 축소
많은 feature(특징)로 구성된 다차원의 데이터 셋의 차원을 축소시킨다.
이를 통해 새로운 차원의 데이터 셋을 구성하고 데이터 밀집도를 낮춘다.
축소 방법
1. feature 선택
모든 feature 중 필요한 것만 선택한다.
중첩되는 변수는 상관 분석을 통해 하나만 선택한다.
2.feature 추출
높은 차원의 feature들을 더 필요한 요소로 추출하는 방법
PCA, factor analysis가 있음. -> 차원 축소 알고리즘
차원이 낮을수록 시각적 데이터 압축으로 표현이 용이하고 컴퓨터 성능에도 무리가 없음
투영
3차원 공간 상의 데이터를 2차원 부분 공간으로 투영하는 방법

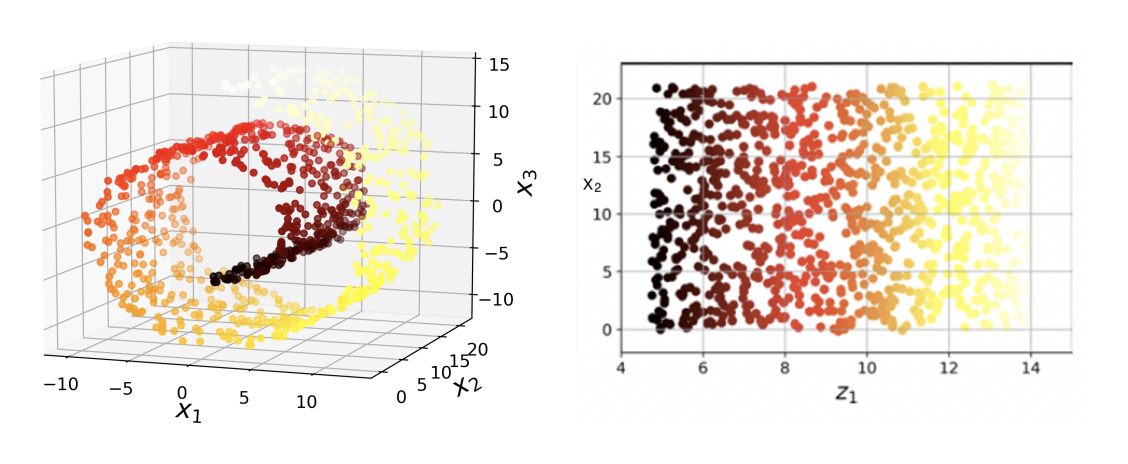
왼쪽 3차원의 데이터 셋을 오른쪽과 같이 2차원에 투영시키는 방법.
각 데이터를 가장 짧은거리인 직선으로 공간에 투영시킨다.
x1, x2, x3 feature인 3차원을 z1, z2로 축소하는게 중요.
매니폴드
고차원 데이터가 있을 때, 이 데이터들을 공간에 뿌린다. 그럼 이 데이터들을 잘 아우르는 subspace가 있을 것이라는 가정에서 학습을 진행하는 방법.
매니폴드를 통해 샘플 데이터의 중요한 특징을 파악할 수 있다.

위 사진은 투영의 올바르지 못한 예이다. 검은색에 가까운 데이터들과 갈색에 가까운 데이터들은 3차원에서 높이가 다름에도 비슷한 위치에 투영되었다. 이런 투영으로 해결할 수 없는 문제를 다루기 위해 매니폴드를 사용한다.
PCA(Principal Component Analysis)
분산?
값들이 얼마나 퍼져있는지에 대한 값, 값이 크면 넓게 퍼져있고, 값이 작으면 좁게 분포되었음을 의미
주성분 분석
여러 변수 간에 존재하는 상관관계를 측정하여 데이터를 대표하는 주성분을 추출해 차원을 축소하는 가장 대표적인 차원 축소 방법이다.
이 방법은 데이터에 가장 가까운 평면을 정의하고 데이터를 그 평면에 투영하는 방법이다. 평면은 2차원을 의미한다. 1차원 직선에 투영할 경우 겹쳐지는 데이터가 존재하기 때문에 분산이 제대로 이뤄지지 않는다.
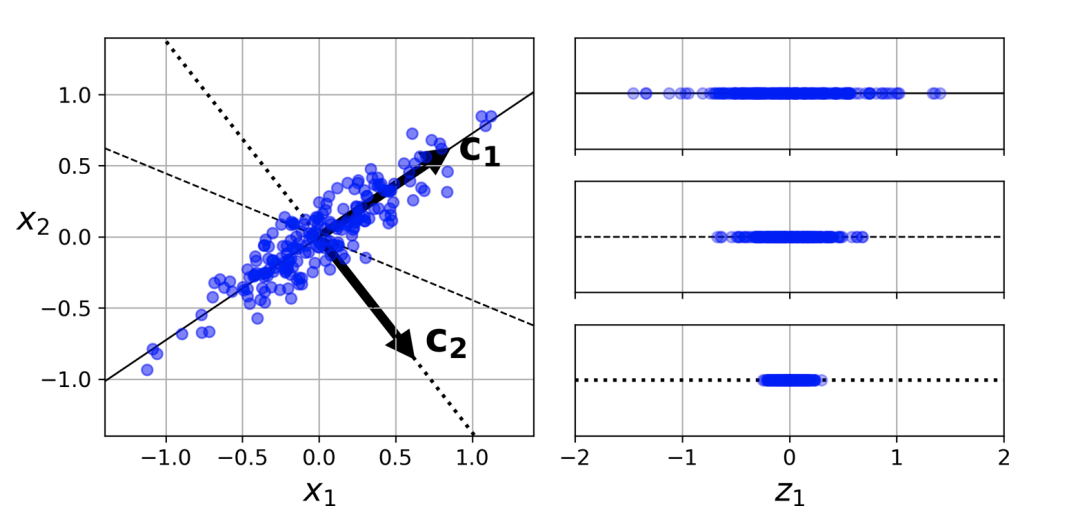
오른쪽 사진의 첫번째는 데이터가 가장 밀집된 c1에 투영한 모습, 세번째는 c1과 수직인 c2에 투영한 모습이다.
c1에 투영한 데이터가 훨신 잘 분산되어 있다.
이런 축을 선택하기 위해선 원본 데이터셋과 사영된 데이터 셋 사이의 평균제곱거리가 최소여야 한다.
그럼 주성분은 뭘 의미할까?
주성분이란 데이터를 투영시킬 수 있는 각 축의 단위 벡터를 말한다.즉, c1,c2 등이 주성분이다.
이런 주성분을 찾는 방법은 다음과 같다.
c1 : 분산을 최대한 보존한 축
c2: 첫째 주성분과 수직을 이루면서 분산을 최대한 보존한 축
c3 : c1,c2와 수직을 이루면서 분산을 최대한 보존한 축
...
이 과정은 차원의 수만큼 진행한다.
주성분을 찾기 위해선 특잇값 분해(SVD) 기법을 이용한다.
2편에 이어서...
'머신러닝' 카테고리의 다른 글
| 머신러닝 / HAI Baseline (0) | 2023.03.27 |
|---|---|
| 머신러닝 / 표준화, 정규화, 스케일링 (0) | 2023.01.16 |
| 머신러닝 / 로지스틱 회귀 케라스 구현 (0) | 2023.01.13 |
| 머신러닝 / 로지스틱 회귀 (0) | 2023.01.13 |
| 머신러닝 / 단순 선형 회귀 케라스 구현 (0) | 2023.01.13 |
- Total
- Today
- Yesterday
- SVM
- one-to-many
- CAN-FD
- SOME/IP
- 딥러닝
- AVB
- 차량 네트워크
- 머신러닝
- 단순선형회귀
- cuckoo
- many-to-many
- HTML
- 로지스틱회귀
- 회귀
- AVTP
- Ethernet
- automotive ethernet
- 차량용 이더넷
- many-to-one
- 논문 잘 쓰는법
- automotive
- PCA
- problem statement
- Python
- porks
- AE
- json2html
- 크로스 엔트로피
- 케라스
- 이상탐지
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
