티스토리 뷰
순회하는 방식에는 3가지가 있다.
1.전위 순회
2.중위 순회
3.후위 순회
루트 노드를 기준으로 루트 노드를 언제 방문하는가의 차이이다.
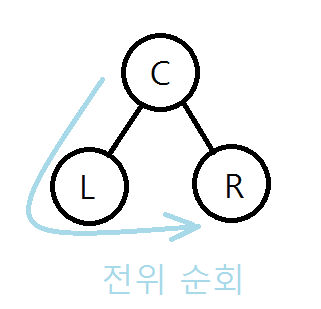
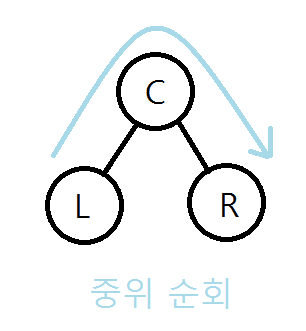
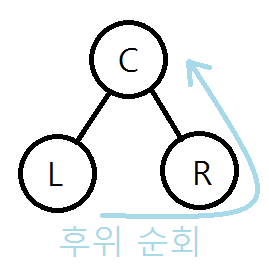
책에서는 중위 순회를 먼저 구현했다.
이렇게 2레벨에서는 간단하지만 3레벨 이상에서는 어떻게 할지 구현해보자.
순회에서 가장 중요한 개념은 재귀 함수이다.
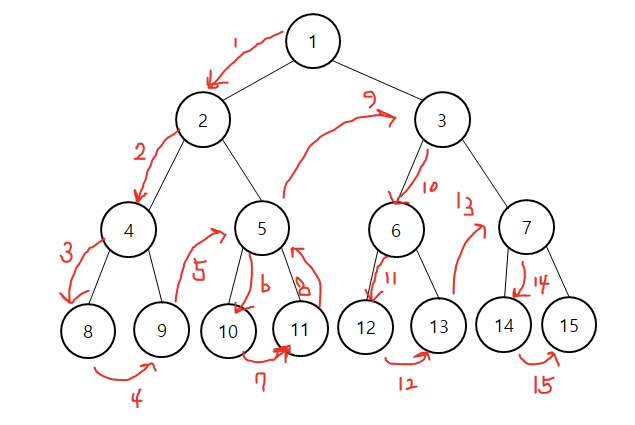
위 그림과 같이 루트 노드 기준 왼쪽 서브 트리를 방문한다.
왼쪽 서브 트리의 맨위를 루트 노드로 생각하고 다시 왼쪽 서브 트리를 방문한다.
그러다 공 노드를 만나게 되면 재귀 함수를 탈출해 루트 노드를 만난다. 다음에 오른쪽 서브 트리를 방문한다.
1.왼쪽 서브 트리 순회
2.루트 노드 방문
3.오른쪽 서브 트리 순회
이런 식이다.
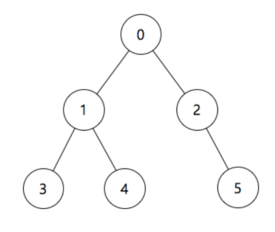

이렇게 0의 왼쪽 1이 루트 노드인 서브 트리 방문 -> 1의 왼쪽 서브 트리 방문(3) -> 루트 노드 1 방문(1) -> 1의 오른쪽 서브 트리 방문(4) -> 루트 노드 0 방문(0) -> 0의 오른쪽 2가 루트 노드인 서브 트리 방문 -> 2의 왼쪽 서브 트리 방문(NULL) ->루트 노드 방문(2)-> 2의 오른쪽 서브 트리 방문(5)
코드로 보면
#include<stdio.h>
#include<stdlib.h>
typedef int BTData;
typedef struct _bTreeNode{
BTData data;
struct _bTreeNode * left;
struct _bTreeNode * right;
}BTreeNode;
//노드 생성,노드 초기화
BTreeNode * MakeTreeNode(){
BTreeNode * newNode=(BTreeNode*)malloc(sizeof(BTreeNode));
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
//노드에 저장된 데이터를 반환
BTData GetData(BTreeNode * bt){
return bt->data;
}
//노드에 데이터 저장
void SetData(BTreeNode * bt,BTData data){
bt->data = data;
}
//왼쪽 서브 트리 주소값 반환
BTreeNode * GetLeftSubTree(BTreeNode * bt){
return bt->left;
}
//오른쪽 서브 트리 주소값 반환
BTreeNode * GetRightSubTree(BTreeNode * bt){
return bt->right;
}
//메인 트리와 왼쪽 서브 트리를 연결한다.
void MakeLeftSubTree(BTreeNode * main,BTreeNode * sub){
if(main->left != NULL)
free(main->left);
main->left = sub;
}
//메인 트리와 오른쪽 서브 트리를 연결한다.
void MakeRightSubTree(BTreeNode * main,BTreeNode * sub){
if(main->right != NULL)
free(main->right);
main->right=sub;
}
//공 노드이면 재귀 함수 탈출 후 다음 라인 실행
void InorderTraverse(BTreeNode * bt){
if(bt == NULL)
return;
InorderTraverse(bt->left);
printf("%d \n",bt->data);
InorderTraverse(bt->right);
}
int main(){
BTreeNode * bt0 = MakeTreeNode();
BTreeNode * bt1 = MakeTreeNode();
BTreeNode * bt2 = MakeTreeNode();
BTreeNode * bt3 = MakeTreeNode();
BTreeNode * bt4 = MakeTreeNode();
BTreeNode * bt5 = MakeTreeNode();
SetData(bt0,0);
SetData(bt1,1);
SetData(bt2,2);
SetData(bt3,3);
SetData(bt4,4);
SetData(bt5,5);
MakeLeftSubTree(bt0,bt1);
MakeRightSubTree(bt0,bt2);
MakeRightSubTree(bt1,bt4);
MakeLeftSubTree(bt1,bt3);
MakeRightSubTree(bt2,bt5);
InorderTraverse(bt0);
//bt1의 왼쪽 자식 노드의 데이터 출력
//printf("%d \n",GetData(GetLeftSubTree(bt1)));
//bt2의 오른쪽 자식 노드의 데이터 출력
//printf("%d \n",GetData(GetRightSubTree(bt2)));
}
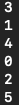
결과도 잘 나온다.
이번엔 전위 순회이다.
전위 순회와 중위 순회의 차이점은 루트 노드를 언제 방문하는가 차이이다.
따라서 코드에서도 그 점만 바꿔주면 된다.
void InorderTraverse(BTreeNode * bt){
if(bt == NULL)
return;
printf("%d \n",bt->data); //루트 노드를 먼저 방문
InorderTraverse(bt->left);
InorderTraverse(bt->right);
}
이렇게 바꿔주기만 하면 된다.
후위 순회도
void InorderTraverse(BTreeNode * bt){
if(bt == NULL)
return;
InorderTraverse(bt->left);
InorderTraverse(bt->right);
printf("%d \n",bt->data); //루트 노드를 마지막에 방문
}
이렇게 바꿔준다.
이번엔 함수 포인터를 활용해본다.
위 코드에서는 단지 출력으로 노드 방문을 표시했지만 함수 포인터를 사용하면 출력 말고도 다른 동작들이 추가된 함수를 사용할 수 있다.
#include<stdio.h>
#include<stdlib.h>
typedef int BTData;
typedef struct _bTreeNode{
BTData data;
struct _bTreeNode * left;
struct _bTreeNode * right;
}BTreeNode;
//노드 생성,노드 초기화
BTreeNode * MakeTreeNode(){
BTreeNode * newNode=(BTreeNode*)malloc(sizeof(BTreeNode));
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
//노드에 저장된 데이터를 반환
BTData GetData(BTreeNode * bt){
return bt->data;
}
//노드에 데이터 저장
void SetData(BTreeNode * bt,BTData data){
bt->data = data;
}
//왼쪽 서브 트리 주소값 반환
BTreeNode * GetLeftSubTree(BTreeNode * bt){
return bt->left;
}
//오른쪽 서브 트리 주소값 반환
BTreeNode * GetRightSubTree(BTreeNode * bt){
return bt->right;
}
//메인 트리와 왼쪽 서브 트리를 연결한다.
void MakeLeftSubTree(BTreeNode * main,BTreeNode * sub){
if(main->left != NULL)
free(main->left);
main->left = sub;
}
//메인 트리와 오른쪽 서브 트리를 연결한다.
void MakeRightSubTree(BTreeNode * main,BTreeNode * sub){
if(main->right != NULL)
free(main->right);
main->right=sub;
}
//함수 포인터형 visitfuncptr의 정의
typedef void VisitFuncPtr(BTData data);
//중위 순회
//공 노드이면 재귀 함수 탈출 후 다음 라인 실행
//action에 들어간 함수는 void형,매개변수가 1개 여야함
void InorderTraverse(BTreeNode * bt,VisitFuncPtr action){
if(bt == NULL)
return;
InorderTraverse(bt->left,action);
action(bt->data); //출력 외의 다른 기능을 구현하기 위해 함수 포인터를 사용
InorderTraverse(bt->right,action);
}
//전위 순회
void PreorderTraverse(BTreeNode * bt,VisitFuncPtr action){
if(bt == NULL)
return;
action(bt->data);
PreorderTraverse(bt->left,action);
PreorderTraverse(bt->right,action);
}
//후위순회
void PostorderTraverse(BTreeNode * bt,VisitFuncPtr action){
if(bt == NULL)
return;
PostorderTraverse(bt->left,action);
PostorderTraverse(bt->right,action);
action(bt->data);
}
void ShowData(int data){
printf("%d ",data);
}
int main(){
BTreeNode * bt0 = MakeTreeNode();
BTreeNode * bt1 = MakeTreeNode();
BTreeNode * bt2 = MakeTreeNode();
BTreeNode * bt3 = MakeTreeNode();
BTreeNode * bt4 = MakeTreeNode();
BTreeNode * bt5 = MakeTreeNode();
SetData(bt0,0);
SetData(bt1,1);
SetData(bt2,2);
SetData(bt3,3);
SetData(bt4,4);
SetData(bt5,5);
MakeLeftSubTree(bt0,bt1);
MakeRightSubTree(bt0,bt2);
MakeRightSubTree(bt1,bt4);
MakeLeftSubTree(bt1,bt3);
MakeRightSubTree(bt2,bt5);
//VisitFuncPtr = showData;
InorderTraverse(bt0,ShowData);
//bt1의 왼쪽 자식 노드의 데이터 출력
//printf("%d \n",GetData(GetLeftSubTree(bt1)));
//bt2의 오른쪽 자식 노드의 데이터 출력
//printf("%d \n",GetData(GetRightSubTree(bt2)));
}'c언어 > 자료구조' 카테고리의 다른 글
| [자료구조]힙의 변경 (0) | 2021.02.05 |
|---|---|
| [자료구조]우선순위 큐의 이해 (0) | 2021.02.01 |
| [자료구조]이진 트리 구현 (0) | 2021.01.31 |
| 트리의 개요 (0) | 2021.01.31 |
| 덱의 이해와 구현 (0) | 2021.01.31 |
- Total
- Today
- Yesterday
- SVM
- AVTP
- Python
- 회귀
- CAN-FD
- 이상탐지
- SOME/IP
- 케라스
- problem statement
- automotive
- one-to-many
- 딥러닝
- 머신러닝
- many-to-many
- 차량 네트워크
- 논문 잘 쓰는법
- PCA
- 논문 작성
- related work
- AE
- 로지스틱회귀
- cuckoo
- HTML
- Ethernet
- porks
- AVB
- automotive ethernet
- many-to-one
- 차량용 이더넷
- 단순선형회귀
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
