티스토리 뷰
피드 포워드 신경망(FFNN)
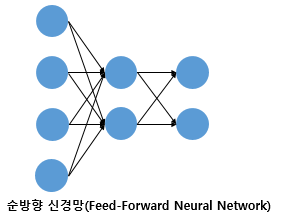
입력층에서 출력층 방향으로 연산이 앞으로 전개되는 신경망을 피드 포워드 신경망이라고한다.

RNN은 은닉층의 출력값을 출력으로도 보내지만, 은닉층의 출력값이 다시 은닉층의 입력으로 사용되는 신경망이다.
전결합층(Dense layer)
MLP의 은닉층과 출력층의 뉴런은 이전 층의 모든 뉴런과 연결이 되어있는 층을 전결합층이라고 한다. 위 사진 모두 은닉층과 출력층이 이전의 모든 뉴런과 연결되어 있는 전결합층이다.
활성화 함수

은닉층과 출력층의 뉴런에서 출력값을 결정하는 함수를 활성화 함수라고 한다. or, and, nand 게이트의 경우엔 계단 함수를 통해서 출력값을 0이나 1로 결정했다.
활성화 함수의 특징은 비선형 함수여야 한다.
선형 함수는 입력의 상수배만큼 출력값이 변하는 일차원 그래프(f(x)=wx+b)를 의미한다.
반면 비선형 함수는 은닉층을 계속해서 쌓는 모습이다. 활성화 함수가 f(x)=wx라고 가정할 때, 은닉층 2개를 더 쌓으면
y(x)=f(f(f(x)))가 되고, 이는 w(w(w(x)))이다.w^3을 k라고 정의하면 y(x)=kw가 되고 이는 일차원 그래프이기 때문에 활성화 함수가 선형 함수이면 은닉층을 추가하는 의미가 없어진다.
그렇다고 선형함수를 은닉층에서 아예 사용하지 않는건 아니다. 학습 가능한 가중치를 새로 만들기 위해 선형 함수를 사용하는 경우도 있다. 이런 층은 선형층이나 투사층이라고 부른다.
import numpy as np
import matplotlib.pyplot as plt
def step(x):
return np.array(x > 0, dtype=np.int)
x = np.arange(-5.0,5.0,0.1) #-0.5부터 5.0까지 0.1 간격으로 생성
y = step(x)
plt.title('Step Function')
plt.plot(x,y)
plt.show()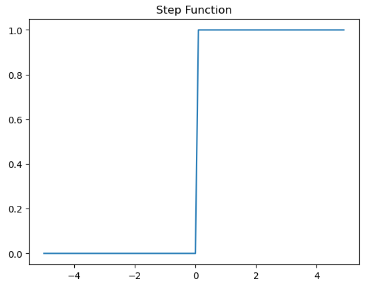
시그모이드 함수와 기울기 소실

인공 신경망은 입력에 대해서 순전파 연산을 하고, 순전파 연산을 통해 나온 예측값과 실제값의 오차를 손실 함수를 통해 계산하고, 이 손실을 미분을 통해 기울기를 구하고, 이를 통해 출력층에서 입력층 방향으로 가중치와 편향을 업데이트하는 역전파를 수행한다. 간단히 말해서 가중치와 편향을 업데이트 하는 과정이다. 여기서 경사 하강법을 사용합니다.
def sigmoid(x):
return 1/(1+np.exp(-x)) #로그함수 그래프를 그려줌
x = np.arange(-5.0,5,0.1)
y = sigmoid(x)
plt.plot(x,y)
plt.plot([0,0],[1.0,0.0],':') #x축 0.0에서 y축1.0부터 0.0 길이의 점선 추가
plt.show()
위 그래프는 시그모이드 함수의 그래프이다. 시그모이드 함수는 출력 값이 0이나 1에 가까워지면 기울기가 완만해진다.
주황색 부분은 미분값이 0에 가까운 작은 값이고, 초록색 구간에서 미분값은 최대 0.25이다.
시그모이드 함수를 활성화 함수로 사용해 층을 쌓으면 가중치와 편향을 업데이트하는 과정인 역전파 과정에서 0에 가까운 값이(최대 0.25로 작은 값이기 때문에) 누적되면서, 앞단에는 기울기가 잘 전달되지 않는다. 이러한 현상을 기울기 소실이라고 한다.

기울기 소실 문제로 인해 출력층과 가까운 은닉층에는 기울기가 잘 전파되지만, 앞단은 기울기가 잘 전달되지 않는다. 따라서 시그모이드 함수의 은닉층에서의 사용은 지양하고 주로 이진 분류를 위한 출력층에서 사용한다.
하이퍼볼릭탄젠트 함수
x = np.arange(-5.0,5.0,0.1)
y = np.tanh(x)
plt.plot(x,y)
plt.plot([0,0],[1.0,-1.0],':')
plt.axhline(y=0,color='orange',linestyle='--')
plt.show()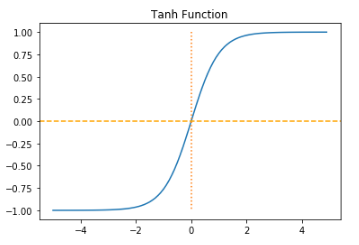
하이퍼볼릭탄젠트 함수도 -1과 1에 가까운 출력값을 출력할 때 기울기 손실 문제가 발생하지만 하이퍼볼릭탄젠트 함수의 경우엔 0을 중심으로 하고있고, 미분했을 때의 최대값이 1로 시그모이드 함수보다 크다.
렐루 함수
은닉층에서 가장 인기있는 함수로 f(x)=max(0,x)로 간단하다.
def relu(x):
return np.maximum(0,x)
x = np.arange(-5.0,5.0,0.1)
y = relu(x)
plt.plot(x,y)
plt.plot([0,0],[5.0,0.0],':')
plt.show()
렐루 함수는 음수에서는 0만을 출력하고 양수에서는 입력값을 그대로 반환한다. 따라서 미분값이 양수에서는 1이다. 하지만 음수의 입력값에서는 미분값이 0이라는 문제점이 있다.
리키렐루
렐루 함수를 보완하기 위한 함수로 입력값이 음수일 경우 미분값을 아주 작은 수로 반환하도록 한다.
f(x)=max(ax,x) 모양이며 a값이 leaky 값을 결정한다. 이 값이 기울기이며 일반적으로 0.01의 값을 가진다.
a = 0.1
def leaky_relu(x):
return np.maximum(a*x,x)
x = np.arange(-5.0, 5.0, 0.1)
y = leaky_relu(x)
plt.plot(x,y)
plt.plot([0,0],[5.0,0.0],':')
plt.show()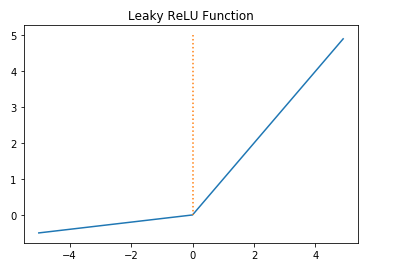
소프트맥스 함수
은닉층에서는 주로 렐루 함수를 사용하지만 출력층에서는 소프트맥스 함수를 주로 사용한다. 시그모이드 함수가 이진 분류 문제에서 사용한다면 소프트맥스 함수는 세가지 이상의 선택지 중 하나를 고르는 다중 클래스 분류 문제에 주로 사용한다.
x = np.arange(-5.0,5.0,0.1)
y = np.exp(x) / np.sum(np.exp(x))
plt.plot(x,y)
plt.show()
'머신러닝 > 딥러닝' 카테고리의 다른 글
| 케라스 훑어보기 (1) | 2022.09.16 |
|---|---|
| 과적합을 막는 방법 (0) | 2022.09.16 |
| 손실 함수, 옵티마이저, 에포크 (1) | 2022.09.15 |
| 행렬곱으로 이해하는 신경망 (0) | 2022.09.15 |
| 퍼셉트론 (0) | 2022.09.15 |
- Total
- Today
- Yesterday
- AVB
- 로지스틱회귀
- Ethernet
- 차량 네트워크
- Python
- cuckoo
- 회귀
- PCA
- json2html
- many-to-one
- automotive
- HTML
- SOME/IP
- AVTP
- 단순선형회귀
- CAN-FD
- automotive ethernet
- 차량용 이더넷
- many-to-many
- 머신러닝
- 논문 잘 쓰는법
- AE
- 케라스
- problem statement
- 이상탐지
- porks
- 크로스 엔트로피
- SVM
- 딥러닝
- one-to-many
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
