티스토리 뷰
SVM이란 N차원 공간을 N-1차원으로 나누는 분류 기법이다.

이렇게 0과 1을 나누는 최적의 경계를 찾는 기법을 말한다.
경계를 기준으로 각 클래스의 말단 데이터(support vector)와 경계 사이의 공간을 마진이라고 하고 이 마진을 최대화 하는 경계를 찾는다. 마진이 최대화해야 robustness값이 최대가 되기 때문이다. robust(튼튼한)의 의미는 최적으로 일반화를 하여 이상치(outlier)의 값이 들어와도 크게 흔들리지 않는다는 말이다. 파란 클래스와 빨간 클래스의 값들이 경계쪽으로 조금 더 다가와도 경계에 크게 영향을 미치않아야한다. 새로운 데이터가 들어와도 경계에 영향을 미치지 않을 수 있다.
N차원은 N-1차원으로 나눈다는 의미를 생각해보면 위 그림에서 2차원 공간을 분류하기 위해서 1차원인 직선 경계를 찾았다.
다음 그림도 3차원 공간을 나누는 2차원 평면을 찾았다. 여기서 3차원은 속성을 3개를 사용한 경우이다.
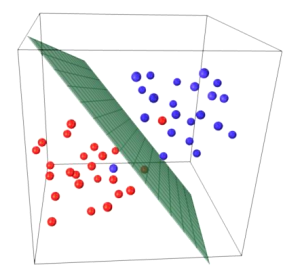
선형 SVM과 비선형 SVM

위 그림은 직선의 형태로 클래스를 분류했다.
이처럼 선형으로 데이터를 분류할 수 있는 경우를 선형 SVM이라고 한다.
하드마진
하드마진은 두 클래스를 분류할 수 있는 최대마진의 초평면을 찾는 방법이다. 쉽게 말해 완벽하게 두개의 클래스를 구분할 수 있는 경계선을 찾는 방법이다.
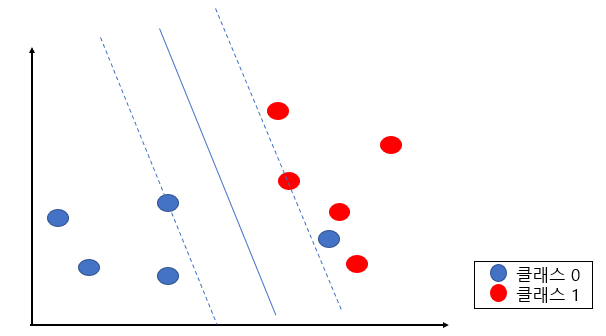
위같은 경우는 파란 클래스가 하나 분류되지 못해서 하드마진으로 볼 수 없다.

w는 가중치이고 b는 편향이다.
그리고 빨간 클래스의 support vector를 지나고 경계선과 평행한 직선 사이의 거리는 1/||w||이고 최대마진의 거리는 2/||w||이다.
경계선 W*X에 대한 공식은 다음과 같다.

경계선 아래 클래스(여기선 파란 클래스)의 값은 다음 공식을 만족한다.

경계선 위 클래스(여기선 빨강 클래스)의 값은 다음 공식을 만족한다.
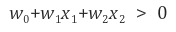

소프트 마진
소프트 마진은 하드마진의 한계를 보완해 나온 방법이다. 하드마진처럼 완벽하게 분류하는 것이 불가능할 때 어느 정도의 오차(노이즈)는 허용하는 방식이다. 오분류를 허용하기 위해 slack variable을 사용하는데 이는 경계선으로부터 노이즈까지의 거리를 측정하기 위해 사용한다.
경계선을 기준으로
경계선을 넘어 완전히 잘못 분류된 경우엔 e > 1
올바르게 분류되었지만 support vector보다 경계선에 가까운 경우엔 0 < e < 1
support vector보다 안쪽에 올바르게 분류된 경우 e = 0
목적함수( 최소값을 찾는 최적화 과정에서 사용하는 함수)에서 slack variable을 C 값으로 총합에 추가해 한계를 줌으로써 조정할 수 있다. 이 값으로 과적합을 제어한다.
C 값이 커지면 오류를 허용하지 않아(하드마진에 가까워짐) 마진이 줄어들어 오류가 적어진다. 하지만 과적합의 위험이 있다.
C 값이 작아지면 마진이 커지지만(오분류를 어느정도 허용함) 과소적합의 위험성이 생긴다.

import sklearn.svm as svm
import sklearn.metrics as mt
import pandas as pd
import numpy as np
from sklearn.model_selection import cross_validate
data = d.load_breast_cancer()
#선형분리
model = svm.SVC(kernel = 'linear')
#scores = cross_validate(model, data.data, data.target, cv=5, return_train_score=True)
scores = cross_val_score(model,data.data, data.target, cv=5)
print(pd.DataFrame(cross_validate(model,data.data, data.target,cv=5)))
print('선형 분리 교차검증 평균:',scores.mean())
#비선형 분리
model = svm.SVC(kernel = 'rbf')
scores = cross_val_score(model,data.data, data.target, cv=5)
result = pd.DataFrame(cross_validate(model, data.data, data.target, cv=5))
print(result)
print('비선형 분리 교차검증 평균:',scores.mean())
선형 분리와 비선형 분리 중 선형 분리가 더 높은 평균값을 보인다. 따라서 breast_cancer 데이터에 대해서는 선형 분리가 더 적합하다.
이번엔 스케일링을 조정해 더 정확하게 값을 내본다.
비선형 SVM(커널 SVM)

위 그림은 비선형으로 데이터를 분류한다. 이런 경우는 비선형 SVM이라고 한다. 선형으로 분류하기 힘든 경우에 특성의 차원을 올려서 구분 경계면을 찾는다. 차원을 올려주는 계산을 담당하는 함수를 기저함수라고 한다.
다음과 같은 지표면의 점들이 있는데 이를 분류할 수 있는 직선은 없다.
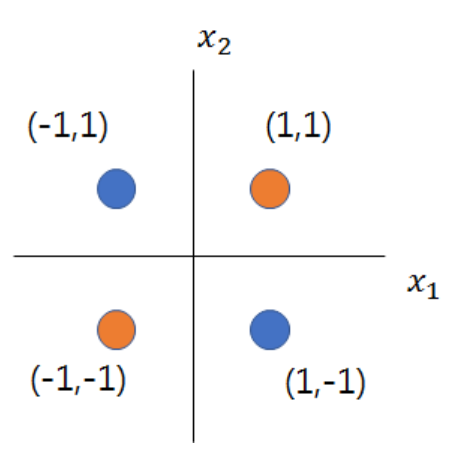
이를 분류하기 위해 다음과 같은 기저함수를 사용해 차원을 바꾼다.

그 결과는

이렇게 되고,

이렇게 3차원으로 표현할 수 있다.
커널 트릭
다항식 커널
선형이 아닌 그래프는 다항식으로 표현해야 된다. 다항식은 많은 특성을 추가하게 되므로 모델의 속도가 느려질 수 밖에 없다.
SVM에서는 커널 트릭이라는 방식을 사용한다. 실제로는 특성을 추가하지 않으면서 다항식 특성을 추가한 것과 같은 결과를 얻을 수 있다.
'머신러닝' 카테고리의 다른 글
| 머신러닝 파라미터와 하이퍼 파라미터 (0) | 2022.10.03 |
|---|---|
| 머신러닝 원핫 인코딩 (1) | 2022.09.30 |
| 머신러닝 get_dummies() (0) | 2022.09.24 |
| 교차검증 (1) | 2022.09.23 |
| 회귀와 분류 차이 (0) | 2022.08.25 |
- Total
- Today
- Yesterday
- 회귀
- 로지스틱회귀
- 크로스 엔트로피
- 머신러닝
- 케라스
- AVB
- SOME/IP
- automotive
- many-to-many
- CAN-FD
- porks
- 차량용 이더넷
- 단순선형회귀
- many-to-one
- SVM
- 차량 네트워크
- Python
- automotive ethernet
- 딥러닝
- json2html
- AE
- HTML
- Ethernet
- one-to-many
- cuckoo
- 이상탐지
- 논문 잘 쓰는법
- AVTP
- PCA
- problem statement
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
