티스토리 뷰
RSA
공개키 암호 알고리즘.
전자서명에서 사용함.
1. B가 공개키와 개인키를 만들어 A에게 공개키를 보낸다.
2. A가 B로부터 받은 공개키를 이용해 보낼 정보를 암호화한다.
3. A가 암호화된 정보를 B에게 보낸다.
4. B가 암호화된 정보를 받고 개인키를 이용해 암호를 해독한다.
(1) 개인키와 공개키 만들기
공개키는 n,e 두 정수로 구성, 개인키는 n,d로 구성.
n구하기
두 소수 p,q를 정하고 n=p*q이다.
e구하기
Φ(n) = (p - 1) * (q - 1) 공식을 이용해 Φ(n)를 구한다.
e는 1 < e < Φ(n) 이고, Φ(n)와 서로소인 e를 정한다.
e는 공개키에 이용된다.
d구하기
(e * d) mod Φ(n) = 1
e * d를 Φ(n)로 나눴을 때 나머지가 1인 d를 구한다. d는 개인키로 사용된다.
ciphertext = Cplaintext = M
암호화하기

위 식을 이용해 M을 C로 암호화한다.
복호화하기

위 식을 이용해 M을 C로 복호화한다.
import random
import math
def gcd(a,b):
while b != 0:
a,b = b,a%b
return a
def prime_num(num):
pm_num = num
for i in range(2,int(math.sqrt(pm_num)) + 1):
if pm_num % i == 0:
return prime_num(pm_num+1)
return pm_num
def get_public_key_e(euler):
e = 2
while e<euler and gcd(e,euler) != 1:
e += 1
return e
def get_private_key_d(e,euler):
d = 1
while (e*d) % euler != 1 or d == e:
d = d+1
return d
def encrypt(pk,m):
n,e = pk
#C = M^e mod n
C = [(ord(char) ** e) % n for char in m]
return C
def main():
m = input("enter plaintext : ")
pp = prime_num(random.randrange(1,20))
pq = prime_num(random.randrange(1,20))
print("(p , q) = ("+str(pp)+","+str(pq)+")")
#get public_key
n = pp*pq
print("n = ",str(n))
euler = ((pp-1)*(pq-1))
print("Φ(n) = ",str(euler))
e = get_public_key_e(euler)
print("e = ",str(e))
print("public_key(n,e) = ("+str(n)+","+str(e)+")")
#get private_key
d = get_private_key_d(e,euler)
print("private_key(n,d) = (" + str(n) + "," + str(d) + ")")
#encrypt
encrypted_M = encrypt((n,e),m)
print("encrypted_M : "+ ''.join(map(lambda x:str(x),encrypted_M)))
if __name__ == "__main__":
main()
AES
대칭키 알고리즘으로 암호화에 사용되는 키 길이는 128(=4워드),192(=6워드),256(=8워드) 비트를 사용할 수 있다.

SPN구조를 사용한다.
SPN구조
substitution과 permuation를 이용해 confusion과 diffusion을 만족시킨다.
confusion(혼돈) : 원문의 내용을 짐작하기 어렵게 만들어야 한다.
diffusion(확산) : 알고리즘의 패턴을 추론하기 어렵게 만들어야 한다.

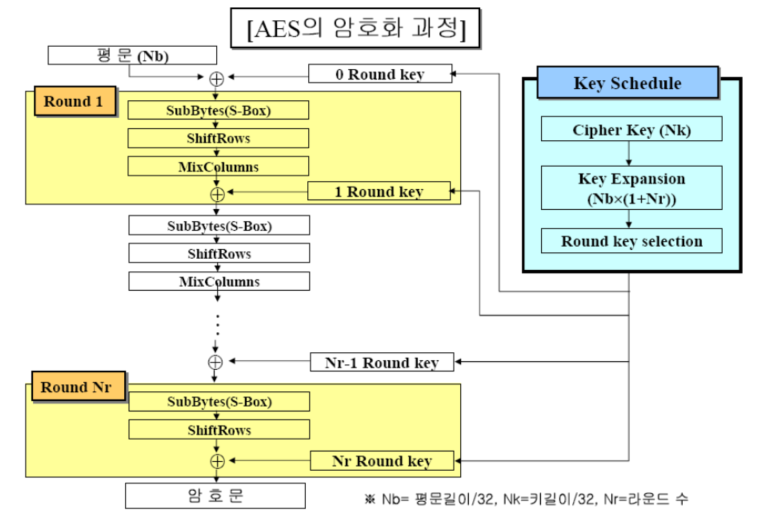
128비트 평문을 입력받고, 키 확장 알고리즘을 통해 생성된 각 라운드 키를 이용해 라운드를 거친다.
여기서 키 확장 알고리즘을 통해 생성된 라운드 키의 수는 총 라운드 수보다 하나 더 많다.
Pre-round transformation에서 필요한 키도 생성하기 때문이다.
Pre-round transformation
128비트 평문과 128비트 길이의 키를 가지고 비트별로 XOR연산을 진행하는 단계
AES 라운드 구성
1. SubBytes
s-box 테이블을 이용해 byte단위 형태로 블록을 교환한다.

state란 byte의 2차원 배열을 의미한다.

이 state의 값을 이용해 아래의 테이블(s-box)에서 일치하는 값을 가져와 대치한다.

00 -> 63, 12 -> C9, 0C -> FE 등으로 대치할 수 있다.
2. ShfitRows (Permutation)
state를 행 단위로 나눈 후 각 행을 왼쪽 방향으로 shift한다.
첫번째 행은 회전하지 않고,
두번째 행은 1byte,
세번째 행은 2byte,
네번째 행은 3byte

3.MixColumns
열 단위 연산을 수행한다. 각각의 열을 상수 행렬과 곱해서 새로운 값을 가지는 열을 반환.

마지막 라운드에서는 MixColumn을 수행하지 않는다.
4. AddRoundKey
state와 128bit 라운드 키를 XOR연산한다.
Key Schedule
키 스케쥴은 key expansion과 roundkey selection으로 이루어져 있다. 먼저 라운드 키를 생성하기 위해 키 확장을 진행한다. 키 확장을 거쳐 생성된 키는 라운드의 마지막 단계 AddRoundKey에 사용된다.
key expansion

key expansion은 워드 단위로 이루어진다.
128비트 = 16바이트 = 4워드 이다.
4개의 워드로 라운드마다 필요한 키를 생성하므로 key expansion이라고 한다.
10라운드를 사용하는 AES128의 경우엔 44개의 워드가 필요한데, 이는 위에서 말했던 Pre-round transformaion에서 사용하기 때문이다.
16바이트의 암호화 키를 워드단위로 나누어 w0,w1,w2,w3을 만든다.
w4를 만들기 위해 마지막 워드 w3을 이용해 RotWord, SubWord를 연산한 후 마지막으로 Round 상수와 XOR 연산을 한다. 이렇게 만들어진 값을 t4로 정하고 아래 연산을 수행한다.
t값은 항상 마지막 워드(w3n+1)를 사용해 계산한다.

w4의 경우 4 mod 4 = 0 이므로 t와 w0을 XOR연산한다.
RotWord
ShiftRow와 비슷한 연산으로, 하나의 word를 왼쪽으로 1byte 이동한다.
SubWord
SubBytes와 비슷한 연산으로, 워드의 각 byte를 S-box를 이용해 대치한 후 출력한다.
RCon(라운드 상수)
4바이트 값으로 가장 오른쪽 3바이트가 모두 0이다.

위의 key expansion을 거친 후 나온 44개의 워드를 4워드 단위로 묶어 라운드에 보내는 작업이 Round key Selection이다.
'프로젝트 > RaaS' 카테고리의 다른 글
| CryptoHunt 정리 (0) | 2022.02.02 |
|---|
- Total
- Today
- Yesterday
- 차량용 이더넷
- 이상탐지
- 크로스 엔트로피
- 케라스
- 머신러닝
- automotive ethernet
- AE
- many-to-many
- 딥러닝
- Ethernet
- problem statement
- json2html
- 회귀
- porks
- AVTP
- 단순선형회귀
- AVB
- PCA
- cuckoo
- CAN-FD
- SOME/IP
- HTML
- 로지스틱회귀
- 차량 네트워크
- 논문 잘 쓰는법
- SVM
- one-to-many
- automotive
- Python
- many-to-one
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
